Image Colorization 🖌️ là quá trình dự đoán màu cho các ảnh đen trắng, giúp tái tạo lại hình ảnh thực tế từ dữ liệu đơn sắc, mang lại trải nghiệm hình ảnh phong phú và sống động. Với đầu vào là một ảnh xám, biểu thị cường độ sáng của ảnh, mô hình sẽ học cách ước tính các kênh màu của ảnh, tạo ra một hình ảnh hợp lý và hài hòa về mặt thị giác. Một trong những bài mà mình được học về chủ đề này đó là bài “Learning Diverse Image Colorization”, mọi người có thể đọc ở đây. BÀI NÀY MÌNH THẤY ADVANCED.

1. Giới thiệu

Task tô màu ảnh thoạt qua nghe hơi nhảm (mình thấy vậy 😐), nhưng thật ra có nhiều ứng dụng cho đời sống hàng ngày của chúng ta, sơ sơ qua thì nó có thể làm cho những ảnh trắng đen trong quá khứ có màu sắc hơn, đối với lĩnh vực ML&DL thì cũng có thể coi như việc tô màu là một cách để chúng ta tăng cường số lượng dữ liệu hiện có (data augmentation) thậm chí ở những lĩnh vực như y khoa cũng sử dụng tới, như là để tăng cường cái sắc độ, giúp cho các bác sĩ nhìn vào dễ chuẩn đoán hơn, và nhiều nhiều cái khác. Thì cụ thể hơn, bài toán tô màu ảnh mình nhắc đến trong bài này là như sau:

Song, đây vẫn là một vấn đề không dễ đễ tiếp cận, bởi vì có rất nhiều cách để sinh ra nhiều màu khác nhau từ một tấm ảnh trắng đen, quan trọng ở đây là màu được tô có nghĩa, và ngoài ra, theo như paper (viết vào năm 2017), tại thời điểm đó, các phương pháp tô màu ảnh còn chưa được tốt cho lắm, bởi vì tại thời điểm đó, các phương pháp cũ chỉ đưa ra được gần như là 1 kết quả duy nhất (tức là chỉ có 1 tấm ảnh màu, nó không đa dạng lắm).

Với cái vấn đề như trên, goal của paper này là thiết kế ra một model có khả năng đa dạng ảnh tô được tô màu hơn (nhưng màu tô vẫn phải hợp lý)

Cái hình dưới đây mình bê từ cái paper ra, họ làm trên bộ dữ liệu LFW (Labeled Faces in the Wild)

Ví dụ như mấy cái hình này của người ta, nó đa dạng hơn hẳn những cái model sẵn có thời bấy giờ, và mọi người lưu ý thêm là sẽ có khả năng rất cao những sample được tạo ra không giống ground truth, nhưng đây không phải vấn đề, mình sẽ đề cập kĩ hơn ở những phần sau.

References:

• Labeled Faces in the Wild - https://vis-www.cs.umass.edu/lfw/
• Learning Diverse Image Colorization - https://arxiv.org/pdf/1612.01958.pdf

2. Ý tưởng

Những bài toán tô màu ảnh có điểm chung trong code đó chính là chúng ta sẽ có một input là ảnh trắng đen (grey-level image) và output là một trường 2 kênh màu thông qua một hàm ánh xạ nào đó. Như đề cập ở trên thì sẽ có vô số ảnh màu khác nhau cho cùng một ảnh đen trắng. Khác nhau ở đây có chăng là ở cường độ của màu dự đoán, ví dụ như một cái sẽ có màu trời đậm hơn, cái còn lại có ảnh màu trời nhạt hơn, v.v… Nghe thì như vậy, những phương pháp deep learning tại thời điểm đó có vẻ không được chuộng cho lắm, song dù sao, objective của bài nghiên cứu này là tạo ra nhiều hình ảnh đa dạng màu sắc, đồng thời có ý nghĩa.

Vấn đề nằm ở chỗ một trường màu nào đó không chỉ phụ thuộc vào những giá trị lân cận, nó còn chịu ảnh hưởng bởi cấu trúc không gian (long-scale spatial structure), điều này khiến cho việc sampling chỉ duy nhất 1 điểm ảnh sẽ làm cho khu vực lân cận điểm ảnh đó không được ăn khớp với nhau, làm cho hình ảnh không được thực tế. Giải pháp là tạo ra được nhiều màu khác nhau nhưng phải cân bằng được giữa ước lượng của điểm ảnh đó với cái cấu trúc không gian ảnh.

2.1 Ý tưởng mô hình

Những cái ở trên đề cập có thể tái hiện dưới công thức toán, mô hình chúng ta mong muốn sẽ là một mô hình xác suất $(P(\mathbf{C}|\mathbf{G}))$ cho trường màu $\mathbf{C}$ dựa trên ảnh xám đầu vào $\mathbf{G}$ và sau đó để tạo ra, chẳng hạn N màu khác nhau đi, lúc này chúng ta sẽ thực hiện lấy mẫu có từ phân phối xác suất vừa đề cập ở trên:

Nhưng do những cái ảnh thường có số chiều rất cao, do đó phân phối của các trường ảnh trong tự nhiên và những đặc trưng của ảnh trắng đen trong không gian nhiều chiều bị phân tán.

Đây là khúc cần lưu ý, tưởng tượng bây giờ bạn đang có 1 chiều dữ liệu thôi, nó đang được hiển thị trên một đường thẳng 1D nào đó, tự nhiên các bạn bỏ vô thêm 2 chiều nữa, lúc này các điểm dữ liệu có thể nằm phân tán ở khắp mọi nơi, như cái hình dưới đây:

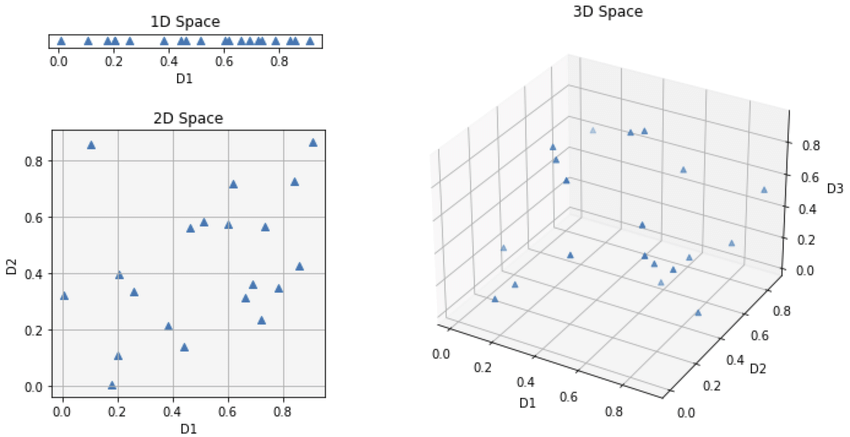
Hãy tưởng tượng các bạn có một túi đầy những đôi tất màu sắc khác nhau, nhưng các bạn không thể nhìn thấy màu sắc, chỉ có thể phân biệt sáng tối giống như ảnh xám. Nhiệm vụ của các bạn là ghép từng đôi tất (grey image) với màu sắc ban đầu của chúng (colorization).

• Cái túi (High-Dimensional Space): Điều này đại diện cho không gian nhiều chiều, nơi mỗi đôi tất được mô tả bằng nhiều đặc điểm ngoài độ tối (kết cấu, độ dày, v.v.). Những đặc điểm này giúp phân biệt các đôi tất, nhưng chúng không cho các bạn biết màu sắc trực tiếp (vì chúng đang nằm trong tối, các bạn chỉ thấy xám đen thôi, có khi thấy toàn màu đen)

• Thách thức (Scattered Distribution): Vấn đề là các đôi tất có màu sắc khác nhau có thể có mức độ tối tương tự. Điều này có nghĩa là các đôi tất (các điểm dữ liệu) được phân tán khắp túi (không gian nhiều chiều). Vì vậy, chỉ bằng cách cảm nhận độ tối, các bạn khó có thể biết chắc chắn mình đang cầm đôi tất màu gì (sự mơ hồ).

• Ánh xạ sang Màu sắc (RGB Space): Các bạn muốn ánh xạ từng đôi tất (thông tin về mức độ xám) sang màu sắc ban đầu của chúng (không gian RGB, thường là 3 chiều cho đỏ, xanh lá và xanh dương). Nhưng sự phân bố rải rác khiến việc ánh xạ này trở nên không rõ ràng. Một đôi tất tối màu có thể có màu đỏ, xanh dương hoặc thậm chí là đen.

Do đó mà người ta mới muốn giảm cái số chiều biểu diễn xuống, cụ thể hơn là họ muốn tìm những cái đặc trưng biểu diễn cho cả $C$ và $G$ để có thể xây dựng được mô hình xác suất có điều kiện và chiến lược của nhóm tác giả là họ sẽ biểu diễn kênh màu $C$ bằng một giá trị $\mathbf{z}$ (một embedding vector trong latent space), biểu diễn này sẽ được học thông qua một mạng VAE. Kế đến họ sử dụng Mixture Density Network (MDN) để có thể học được một mô hình điều kiện:

Đồng thời các biểu diễn đặc trưng của ảnh xám $G$ sẽ được học thông qua một mạng CNN sao cho nó lấy đuộc thông tin biểu diễn của cái ảnh xám đó (VGG cũng được). Cuối cùng, ở giai đoạn inference, họ sẽ lấy N mẫu từ phân phối:

Sau đó sử dụng VAE decoder để lấy được từng kênh màu $\mathbf{C}_k$ cho từng điểm $\mathbf{z}_k$. Đơn giản vậy thôi 🤓

2.2 VAE

Như đã đề cập ở trên, chúng ta mong muốn học một biểu diễn $\mathbf{z}$ có số chiều thấp hơn chiều biểu diễn của trường màu $C$ , trong paper “Auto-Encoding Variational Bayes”, các tác giả có đưa ra giải pháp là chúng ta sẽ tối đa hàm dưới đây theo $\theta$:

Và để đạt được điều này, họ có đặt ra những giả định khác nhau của các phân phối, cụ thể hơn, hậu nghiệm $P(\mathbf{C}|\mathbf{z},\theta)$ sẽ có phân phối Gaussian, tức là $N(\mathbf{C}|f(\mathbf{z}, \theta), \sigma^2)$. Cũng nhờ vậy mà cái vế đầu trong phương trình (4) sẽ trở thành một mạng decoder với hàm loss L2 với công thức:

\(\begin{equation} \|\mathbf{C} - f(\mathbf{z}, \theta)\|^2 \end{equation}\).

Mình thì không rành về toán lắm, nhưng theo mình, với giả định về hậu nghiệm như vậy, sau khi gắn vào phương trình số (4) thì lúc này giá trị trả ra của vế đầu của phương trình đó là:

Cái này cũng đồng thời là 1 dạng kết quả của decode, như vậy kết hợp với $C$ gốc, việc mình kéo cái giá trị loss $L_2$ xuống cũng đồng thời là việc mình kiếm một bộ $\theta$ đủ tốt để $C$ ước lượng có giá trị bằng hoặc gần bằng với $C$. Giống hệt với objective của phương trình số 4, như vậy giả định tiên nghiệm như vậy là hợp lí.

Bên cạnh hậu nghiệm trên, các tác giả cũng đặt ra một giả định khác cho phân phối của $P(\mathbf{z})$ là một phân phối chuẩn tắc, điều đó làm cho vế sau của phương trình (4) khi áp dụng giả định mới này sẽ mang ý nghĩa chúng ta sẽ train 1 mạng encoder có dạng như dưới đây để nó kéo phân phối của $\mathbf{z}$ về với phân phối chuẩn.

Như vậy là tụi mình đã setup xong phần idea của VAE, một vấn đề khác xuất hiện đó là trong mô hình, chúng ta có thực hiện sampling $z$ từ phân phối $Q$ được học ở trên. Vấn đề ở chỗ này đó là trong quá trình train mô hình, chúng ta không có thực hiện backpropagation được, kiểu không có cách nào để backprop qua một sampling node. Để khắc phục điều này, các tác giả có đề xuất một phương pháp đi kèm đó thủ thuật re-parameterization. Mọi người có thể ngó sơ qua hình sau:

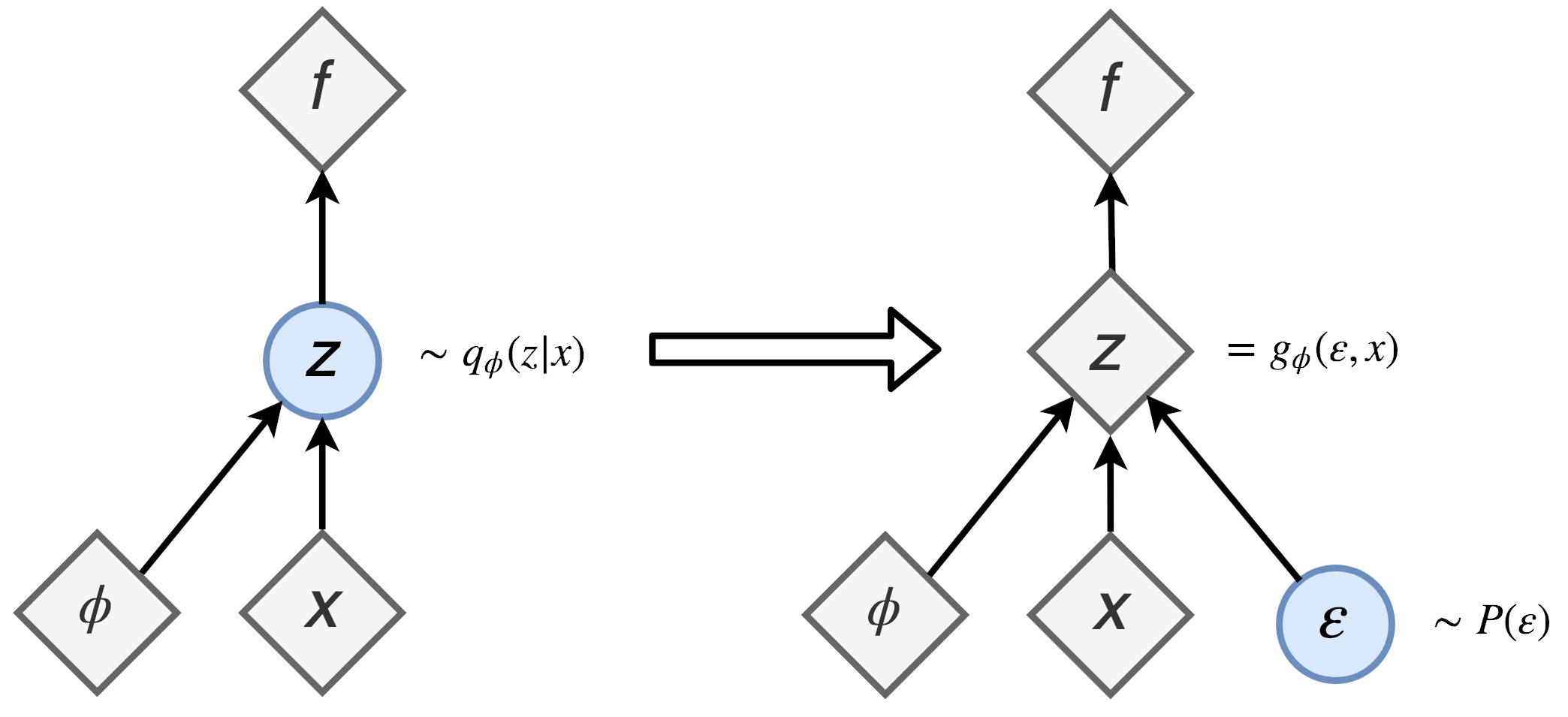
Nói ngắn gọn là nếu chúng ta trực tiếp sampling từ phân phối chuẩn để cho ra vector đại diện $\mathbf{z}$ thì lúc cập nhật trọng số, giá trị đạo hàm sẽ không có đi qua đây được. Cho nên thay vào đó, chúng ta sẽ có phần giá trị $\mu$ và phần phương sai $\sigma^2$ lấy trực tiếp từ 2 layer, phần ngẫu nhiên thì chúng ta sẽ lấy cái phương sai đó nhân với một $\epsilon$ có phân phối chuẩn tắc. Công thức của $\mathbf{z}$ sau khi chúng ta re-parameterization lúc này sẽ là:

2.3 MDN

Các tác giả mong muốn học được một mô hình xác suất có điều kiện giữa ảnh xám $\mathbf{G}$ với embedding vector $\mathbf{z}$. Do đó mà họ sẽ sử dụng Mixture Density Networks (MDN). Điều này cho phép ánh xạ 1-nhiều, điều này hỗ trợ objective của nhóm tác giả khi đề xuất ra paper này đó là MDN cho phép trả ra nhiều vector với nhiều điều kiện khác nhau mặc dù đầu vào cũng cùng là 1 input vector đó, cho phép sự đa dạng mà nhóm tác giả đề cập.

Cụ thể hơn về MDN, đây là một dạng NDE (Neural Density Estimator). Cái NNE này cho phép chúng ta rút ra được cái phân phối dựa vào đầu vào, cụ thể hơn thì mọi người cứ liên tưởng tới bài toán supervised learning nhưng thay vì input là $x$ output là $y$, lúc này ta sẽ có output là phân phối của $y$ theo $x$. Cái NDE này theo mình tìm hiểu thì nó là một paper thuộc NIPS (1998). Về phần Mixutre Density Network (MDN) thì mọi người có thể tìm hiểu ở video này

Một vấn đề với việc chọn phân phối của ouput y theo input x có phân phối Gaussian (unimodal) (giả định như vậy để mấy bài toán hồi quy dễ giải quyết hơn). Nhưng đồng thời giả định đó lại không ổn (dự đoán tệ) cho những bài toán ngược (inverse problem) với multimodal (khác unimodal ở trên) distribution. Đối với những bài toán ngược, dựa vào dữ kiện được cho, sẽ có khả năng chúng ta có rất nhiều kết quả cùng tồn tại, nói cách khác đối với các bài toán này, chúng ta sẽ không có 1 kết quả duy nhất. Do đó mà giả định xác suất $P(\theta | \mathbf{x})$tuân theo phân phối dạng unimodal là không còn chính xác nữa. Do đó mà một phân phối Gaussian, dạng multimodal sẽ phù hợp cho bài toán dạng này.

Chính xác hơn, để có thể mô hình được bài toán ngược với nhiều kết quả phù hợp, chúng ta sẽ sử dụng một mixture model (cụ thể hơn là Gaussian Mixture Model) cho $P(y|x)$, cụ thể hơn trong bài toán tô màu ảnh của chúng ta sẽ là $P(\mathbf{z}|\mathbf{G})$.

Với MDN được xác định như trên, chúng ta sẽ cố gắng làm giảm giá trị loss bằng cách tối thiểu conditional negative log likelihood (tức là tối thiểu $- \log P(\mathbf{z}|\mathbf{G})$). Lúc này, hàm loss cho mô hình MDN sẽ được định nghĩa như bên dưới:

\(\begin{equation} -\log\Sigma_{i=1}^{M} \pi_i(\mathbf{G}, \phi)\mathcal{N}(\mathbf{z}|\mu_i(\mathbf{G},\phi),\sigma) \end{equation}\)

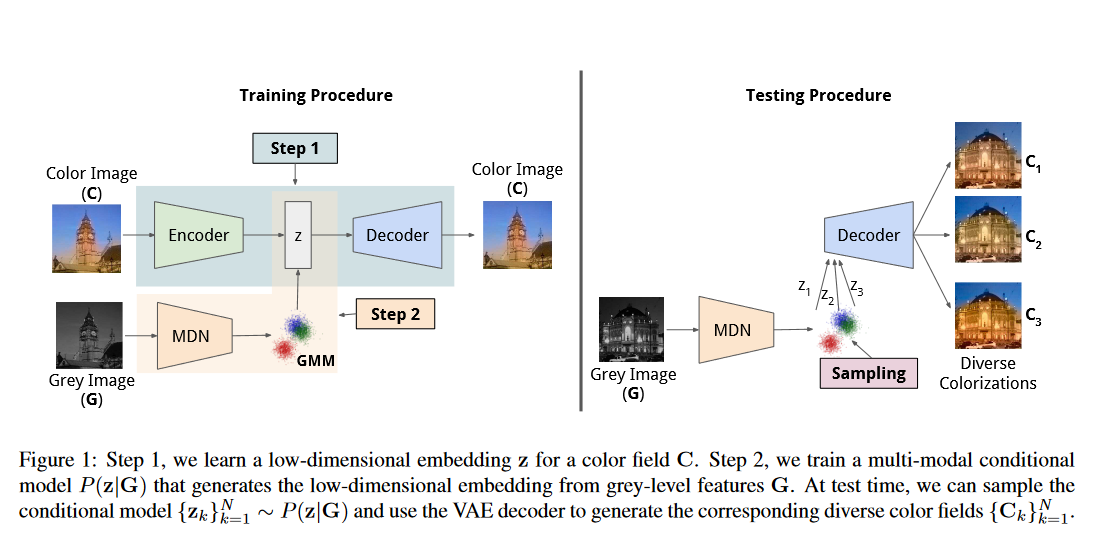
2.4 Huấn luyện

Toàn bộ quá trình huấn luyện mô hình có thể được tóm gọn qua hình dưới đây:

Code

Kết quả

Thảo luận thêm