Fundamental 2: Gaussian Mixture Model and EM algorithm
Published:
Chuyện là mình đang viết cái phần “Paper Explained 6” và nó có nhiều kiến thức bên ngoài quá, nên mình cho thêm 1 blog. Blog này sẽ giải thích về Gaussian Mixture Model và EM algorithm (EM là viết tắc của Expectation-maximization). Blog này sẽ rất là liên quan đến một bài giảng của viện công nghệ IIT, series này rất hay, mọi người có thể xem tập này ở đây.
Giới thiệu:
Trong rất nhiều lĩnh vực khác nhau như xử lý ảnh (image processing), xử lý tín hiệu số (signal processing), khoa học dữ liệu (data science) và nhiều nhiều lĩnh vực khác nữa, chúng ta thường sẽ giả định phân phối của dữ liệu tuân theo một phân phối Gaussian (Normal distribution - phân phối chuẩn). Dưới đây là hình vẽ của một phân phối chuẩn:
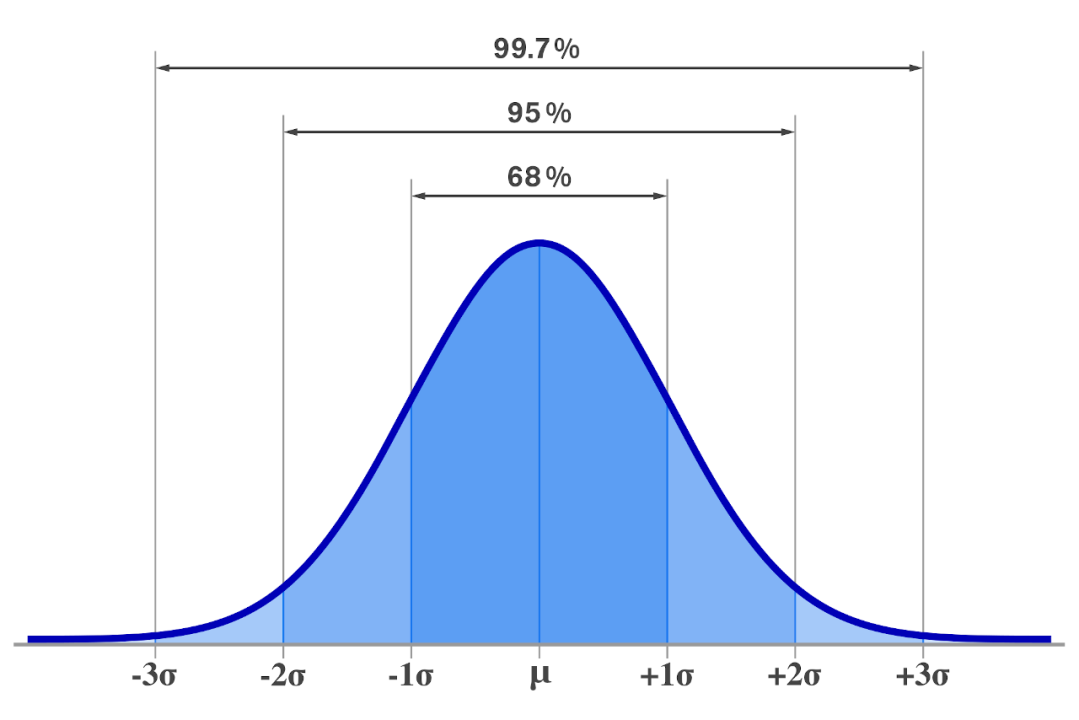
Theo mình tìm hiểu, có 2 nguyên do chính cho việc này:
- Phân phối Gaussian là phân phối gần giống với phân phối trong tự nhiên nhất.
- Công thức toán dễ dàng biến đổi.
Trong nhiều trường hợp, như hình vẽ ở trên, dữ liệu của chúng ta khá đơn giản, rất có khả năng dữ liệu của chúng ta sẽ có phân phối Gaussian. Nhưng cũng có nhiều trường hợp mà phân phối của dữ liệu trở nên phức tạp hơn, điều đó khiến cho việc chúng ta ước lượng phân phối của dữ liệu thực tế là một phân phối Gaussian (hoặc gần giống) thì sẽ không hiệu quả (trong trường hợp này mình đang nói đến unimodal Gaussian distribution với một giá trị $\mu$ và một giá trị $\sigma$). Lúc này, công thức toán của phân phối chuẩn sẽ là như sau:
\[\begin{equation} P(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \end{equation}\]Trong nhiều sách khác, người ta sẽ sử dụng một ký hiệu chung như là: $\mathcal{N}(x|\mu, \sigma^2)$ Tuy nhiên như mình mới nói, do nó không hiệu quả, chúng ta phải cân nhắc thay vì chỉ dùng một phân phối Gaussian để ước lượng, chúng ta có thể sử dụng nhiều phân phối Gaussian (mixture of Gaussians). Cho mọi người dễ hình dung, một cái multimodal Gaussians distribution sẽ nhìn như sau:
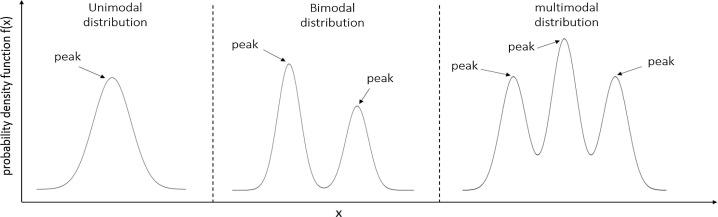
Phần trên là mình đang đề cập về việc đầu vào là biến 1 chiều (univariate variable). Nhưng thông thường chúng ta ít khi làm việc với các giá trị đơn biến (mình thường chỉ gặp lúc làm bài tập về nhà hoặc đọc hiểu tài liệu thôi), thay vào đó, chúng ta thường sẽ làm quen với các dữ liệu nhiều chiều (tức là một biến sẽ có nhiều chiều - multivariate variable). Lúc này, cái phân phối chuẩn ở trên sẽ được biểu diễn khác đi, sang một công thức tổng quát hơn cho phân phối Gauss (multivariate Gaussian distribution):
\[\begin{equation} P(\mathbf{x}) = \frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}} e^{-\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^T \Sigma^{-1} (\mathbf{x}-\mathbf{\mu})} \end{equation}\]Có thể coi multivaritate Gaussian distribution là một dạng tổng quát hơn công thức phân phối chuẩn đơn biến mà mọi người thường gặp. Lưu ý là trong trường hợp sử dụng phân phối Gaussian đa biến, cũng sẽ có trường hợp unimodal, bimodal, multimodal distribution như trường hợp ở trên, nên là đừng nhầm lẫn. Mọi người có thể quan sát hình dưới đây:
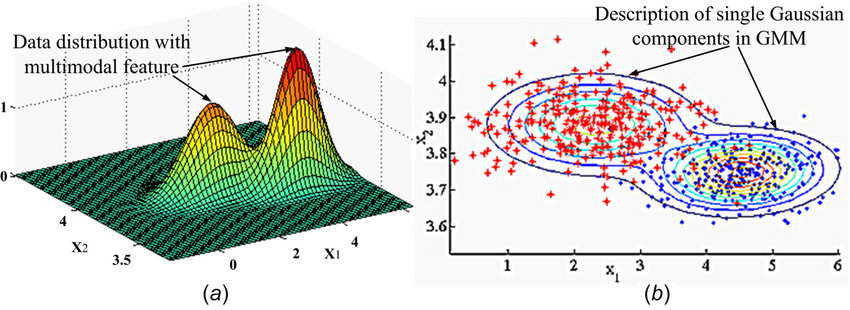
Trong trường hợp của unimodal Gaussian Distribution, chúng ta thường sẽ có 2 tham số, một giá trị $\mu$ để đại diện cho giá trị trung bình và một giá trị $\sigma$ để đại diện cho độ lệch chuẩn, nhưng qua tới trường hợp multimodal Gaussian Distribution, do lúc này chúng ta có nhiều “đỉnh” khác nhau, dẫn tới thay vì giá trị $\mu$ với $\sigma$ đang là dạng số vô hướng, thì bây giờ chúng sẽ được biểu diễn bằng các vector $\mathbf{\mu}$ cho các giá trị trung bình, $\mathbf{\sigma}$ cho các giá trị về độ lệch chuẩn. Còn trong trường hợp biến nhiều chiều, lúc này …
Trong trường hợp chúng ta chỉ có một phân phối Gaussian (unimodal) thì chúng ta có thể xấp xỉ các tham số trong mô hình xác suất bằng phương pháp như ước lượng hợp lý cực đại (Maximum likelihood estimation), nhưng khi gặp phải trường hợp nhiều phân phối Gaussian khác nhau, chúng ta khó có thể làm được như vậy, bởi vì phương pháp MLE này không hoạt động cho multimodal Gaussian Distribution. Do đó chúng ta cần một phương pháp tiếp cận khác là EM (Expectation-maximization).
Lý do cho việc MLE không phải là một phương pháp ước lượng tốt cho mô hình xác suất multimodal Gaussian là bởi vì:
- Objective của MLE là tìm được một bộ tham số tối ưu (vector $\mathbf{\mu}$ và ma trận hiệp phương sai $\mathbf{\Sigma}$) để có thể tối đa khả năng mà dữ liệu được sinh ra từ mô hình xác suất đó.
- Trong trường hợp của unimodal Gaussian distribution, các tham số mà chúng ta mong muốn tìm được trong quá trình ước lượng là bằng đúng với $\mathbf{mu}$ và $\mathbf{\Sigma}$ được sinh ra từ dữ liệu. Nhưng trong trường hợp multimodal Gaussian distribution thì không dễ như vậy, do có nhiều phân phối Gaussian kết hợp lại với nhau, khiến cho việc ước lượng sử dụng MLE không hiệu quả nữa.
GMM (Gaussian Mixture Modal)
Mixture models
Trước khi tìm hiểu sâu hơn về GMM, trước tiên ta phải có một chút hiểu biết về mixture model. Thì Mixture model là một mô hình xác suất có thể giúp chúng ta ước lượng được một phân phối phức tạp trong dữ liệu. Lấy ví dụ như các chỉ số tài chính trong trường hợp thị trường ổn định thì sẽ có phân phối khác với khi thị trường đang gặp khủng hoảng.
Cụ thể hơn, nếu như một biến ngẫu nhiên $X$ tuân theo một phân phối là tổ hợp của $K$ phân phối khác, thì hàm mật độ xác suất Gaussian sẽ là tổng có trọng số của K thành phần mật độ (trong trường hợp các phân phối thành phần tuân theo Gaussian distribution, và đang cân nhắc trường hợp biến một chiều):
\[\begin{equation} P(X = x) = \sum_{k=1}^K w_k \mathcal{N}(x|\mu_k, \sigma_k) \end{equation}\]Ý tưởng đơn giản là vậy, trong phương trình ở trên, cần lưu ý ở những thành phần sau:
- $w_k$ là trọng số của các phân phối thành phần, cái này sẽ có range từ 0 đến 1, bên cạnh đó, tổng của các trọng số này, tức là $\Sigma^K w_k = 1$.
- $\mathcal{N}(x|\mu_k, \sigma_k)$ là các phân phối chuẩn khác nhau.
Như trong hình dưới đây là một phân phối được trộn từ 2 phân phối Gaussian với lần lượt là: $\mu_1 = -1$, $\sigma_1 = 1$ và $\mu_2 = 4$, $\sigma_2 = 1.5$, bên cạnh đó, trọng số cho từng cái lần lượt là: $w_1 = 0.7$, $w_2 = 0.3$.
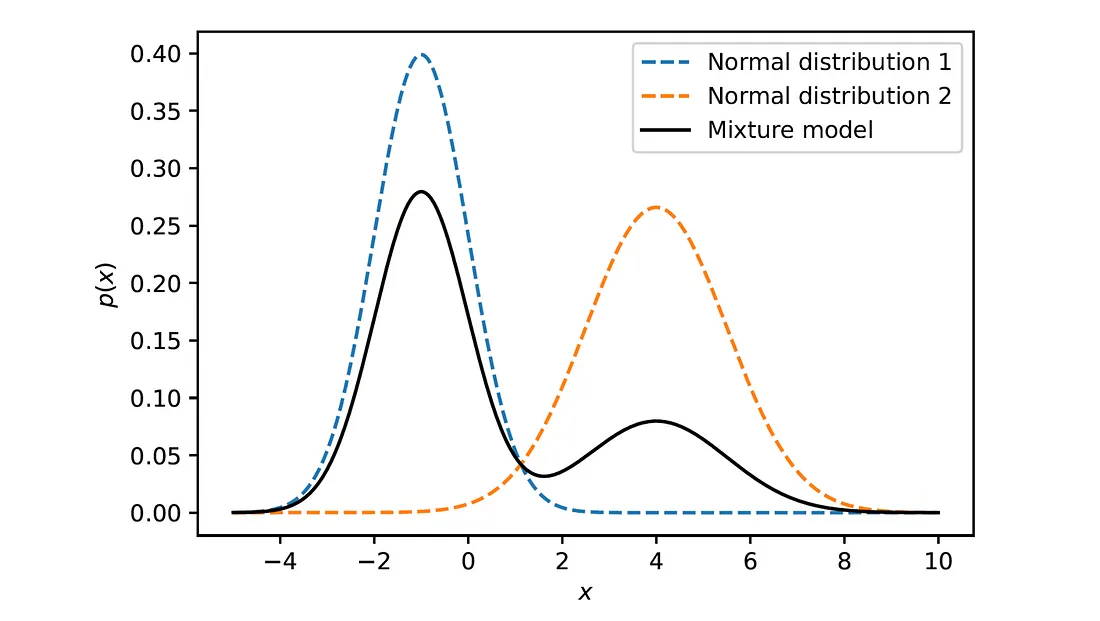
Ưu và nhược điểm khi sử dụng GMMs
EM (Expectation-Maximization)
TLDR: Thuật toán EM gồm 2 bước chính (như tên gọi của nó Expectation và Maximization). và đây là một quá trình lặp đi lặp lại bằng cách kết hợp nhiều phương pháp học không giám sát để tìm ước lượng hợp lý cực đại cho bộ tham số của mô hình. Và thông qua quá trình tối ưu này, thuật toán mong muốn tìm được ước lượng hợp lý cực đại cho bộ tham số với dữ liệu sẵn có. Ngắn gọn 2 bước như sau:
- Bước E: Ước lượng các tham số bị mất trong bộ dữ liệu.
- Bước M: Tối đa các tham số trong mô hình với số dữ liệu sẵn có
Như đã nói ở trên, trong trường hợp chúng ta ước lượng dữ liệu cho GMM,
Dưới đây là toàn bộ quá trình áp dụng EM để tìm ra bộ tham số phù hợp cho mô hình xác suất GMM:
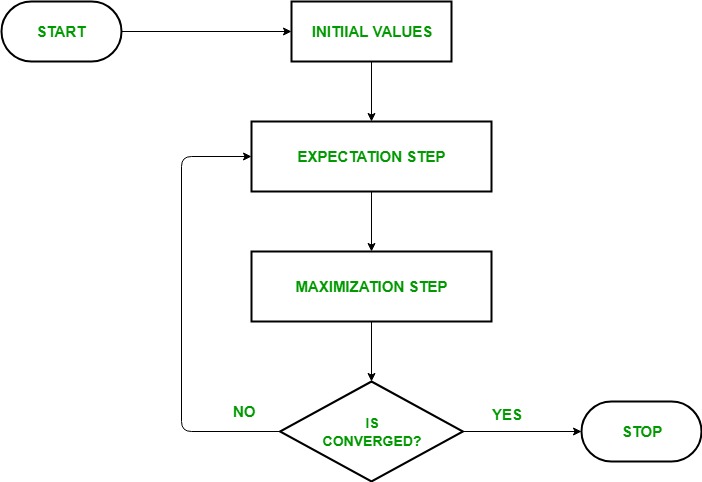
Mình xin được phép giải thích rõ hơn:
- Khởi tạo bộ tham số $\Theta^{old}$
- E-Step: Đánh giá xác suất có điều kiện $p(\mathbf{Z}|\mathbf{X}, \Theta^{old})$ và thực hiện tính công thức sau:
- M-Step: Tối đa
- Đánh giá giá trị log likelihood rồi kiểm tra tính hội tụ của mô bộ tham số này. Nếu bộ tham số mới này chưa dẫn tới hội tụ, lúc này ta gán $\Theta^{old}$ thành giá trị của $\Theta^{new}$ rồi quay trở lại bước 2.
Trong việc chúng ta ước lượng GMM, quá trình trên sẽ chuyển thành như sau: